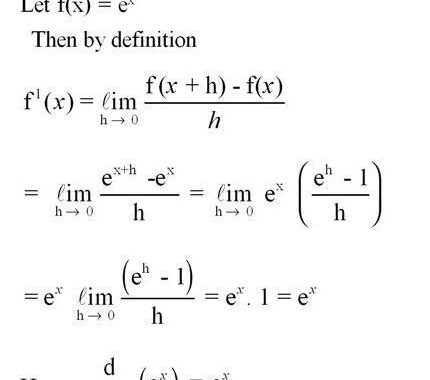Have you ever glanced at a scientific calculator and noticed a mysterious symbol, the letter “e,” sometimes accompanied by a multitude of digits? It poses a playful question: What exactly does this enigmatic “e” signify in our numerical adventures? Understanding this concept requires delving into the realm of mathematics, specifically calculus and exponential functions.
At its core, “e” represents Euler’s number, an irrational constant approximately equal to 2.71828. Its significance extends far beyond mere calculations, as it serves as the foundation for natural logarithms and exponential growth. This unique number emerges naturally in various mathematical contexts, such as compound interest, population models, and even radioactive decay. In essence, “e” encapsulates the idea of continuous growth, making it a critical player in calculus.
When you encounter “e” on a calculator, it typically indicates the function related to this exceptional constant. For instance, calculators often utilize “e” in operations involving exponential functions, allowing users to compute values of the form e^x, where “x” can be any real number. So why might this be a challenge? Consider transforming everyday scenarios into mathematical expressions. Imagine calculating the growth of an investment over time using continuous compounding. Here, “e” becomes indispensable, transforming theoretical concepts into tangible results.
To employ “e” effectively, one must engage with its properties. The function f(x) = e^x serves as the basis for exponential growth. Its unique characteristics include the fact that the slope of the curve at any point equals its value at that point. This inherent property makes “e” exceptionally vital in various fields, including economics, biology, and physics. When you use a calculator, typing “e^2” will yield an approximation of 7.389, demonstrating how foundational “e” is in contexts involving growth and decay.
As you explore further, you may encounter logarithmic functions, specifically the natural logarithm denoted as ln(x). This logarithm utilizes “e” as its base, creating a powerful tool for unraveling complex equations. The relationship between exponentials and logarithms underscores the significance of “e” in mathematical discourse.
In conclusion, the appearance of “e” on your calculator is a gateway into the fascinating world of mathematics, beckoning you to explore exponential functions and their applications. A playful challenge awaits in the form of practical problems that can be solved with the knowledge of “e.” From finance to natural sciences, understanding this mathematical constant empowers you to tackle real-world scenarios with confidence.