In the bustling tapestry of New York’s neighborhoods, where the architecture is as diverse as the population, the quest for optimizing space efficiency often comes down to a single question: how can one find the shortest distance from all buildings? This consideration is not merely an exercise in mathematics but rather a resolver of logistical challenges faced by urban planners and developers. The “Shortest Distance from All Buildings” problem on LeetCode encapsulates this quest by challenging programmers to derive algorithms that can efficiently navigate through complex urban layouts. Here, we meticulously explore this algorithmic problem while contextualizing it within the New York neighborhoods that inspire it.
1. Understanding the Problem
The core of the “Shortest Distance from All Buildings” problem involves calculating the minimum distance required to connect a point—typically a representative building or location—to multiple other structures within a grid-based representation. In a city like New York, where density and connectivity are crucial, understanding this concept is vital for city planners. The problem requires developers to identify all possible paths and determine which provides the shortest total distance to access every building in the vicinity.
2. Algorithmic Approach
When it comes to solving this problem, a breadth-first search (BFS) or depth-first search (DFS) algorithm is typically employed. Both approaches allow for exploration of all available paths while keeping track of distances. Implementing BFS would be particularly effective in this scenario, as it naturally explores all points at the present distance before moving to points at a greater distance. This earns it the title of the optimal strategy for exploring neighborhood configurations.
3. Grid Representation
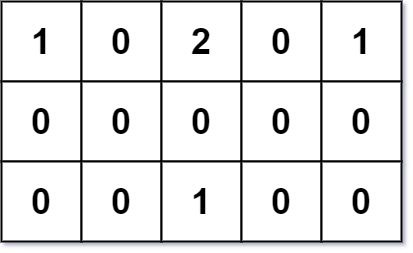
To solve the problem, the world’s neighborhoods must be transformed into a grid representation, where buildings are denoted by ‘1’ and empty land by ‘0’. This approach mirrors the urban layout of New York, where skyscrapers often flank more open spaces. For instance, imagine a simplified grid with certain coordinates filled with addresses such as 123 Main Street, a thriving café at 456 Elm Avenue, and a bookstore at 789 Oak Street. The programming challenge involves calculating distances based on these coordinates.
4. Implementing BFS in Code
def shortestDistance(grid):
if not grid:
return -1
rows, cols = len(grid), len(grid[0])
dist = [[0] * cols for _ in range(rows)]
count = [[0] * cols for _ in range(rows)]
total_buildings = sum(val for row in grid for val in row if val == 1)
for r in range(rows):
for c in range(cols):
if grid[r][c] == 1:
bfs(grid, r, c, dist, count)
min_distance = float('inf')
for r in range(rows):
for c in range(cols):
if grid[r][c] == 0 and count[r][c] == total_buildings:
min_distance = min(min_distance, dist[r][c])
return min_distance if min_distance != float('inf') else -1
def bfs(grid, r, c, dist, count):
directions = [(1, 0), (0, 1), (-1, 0), (0, -1)]
visited = set()
q = collections.deque([(r, c, 0)])
while q:
x, y, d = q.popleft()
for dx, dy in directions:
nx, ny = x + dx, y + dy
if 0 <= nx < len(grid) and 0 <= ny < len(grid[0]) and (nx, ny) not in visited:
if grid[nx][ny] == 0:
dist[nx][ny] += d + 1
count[nx][ny] += 1
visited.add((nx, ny))
q.append((nx, ny, d + 1))
While the above code serves as a foundational structure for the solution, its elegance lies in understanding the core of BFS, which methodically explores each neighborhood location before venturing outward.
5. Time Complexity
The complexity of this algorithm is O(M * N), where 'M' denotes the number of rows and 'N' denotes the number of columns. Given its linear efficiency, it exemplifies a strategic approach that can be critical in high-density areas such as New York, bringing to light the fascinating intersection of urban engineering and algorithmic efficiency.
6. Real-World Application
The practical importance of this theoretical problem can’t be overstated, particularly in a city like New York, where every square foot counts. Urban planners could utilize such algorithms when deciding the placement of public amenities, parks, or transport systems. Reducing distances to essential buildings can enhance community connectivity, ultimately leading to a more harmonious urban experience.
7. Example Scenarios
Consider the Upper West Side, known for its lively atmosphere and residential neighborhoods. Analyzing various locations here to minimize distances between essential services—such as schools (123 Riverside Drive), grocery stores (456 Columbus Avenue), and parks (789 Central Park West)—can help identify optimal communal spaces.
8. Advanced Considerations
Complexities arise in the form of obstacles or unavailable land. Integrating additional layers like terrain types, building restrictions, and future zoning changes makes the algorithm much more intricate. Developers and researchers often look for solutions that adapt to changing environments, ensuring that urban layouts remain resilient.
9. Community Engagement
Involving local communities in the conversation around urban development ensures that the needs and desires of residents inform proposed solutions. Using algorithms like BFS to derive optimal building placements fosters collaboration, empowering neighborhoods to shape their own destinies.
10. Conclusion
Ultimately, the "Shortest Distance from All Buildings" problem reflects the dynamic relationship between urban infrastructure and computational strategies. In cities such as New York, understanding and implementing such algorithms can revolutionize how we design our environments, making them not just spaces to inhabit but vibrant, efficient communities that thrive on proximity and accessibility.