The phrase “less than” serves as a fundamental comparative expression in both mathematical and everyday discourse. It signifies a relational distinction, where one quantity, concept, or item is inferior in value or magnitude to another. This term is frequently used across various domains such as mathematics, economics, and qualitative assessments. At its core, the concept elucidates the idea of numerical disparity and inequality, making it integral to understanding relationships among entities.
In mathematical contexts, “less than” is represented by the symbol “
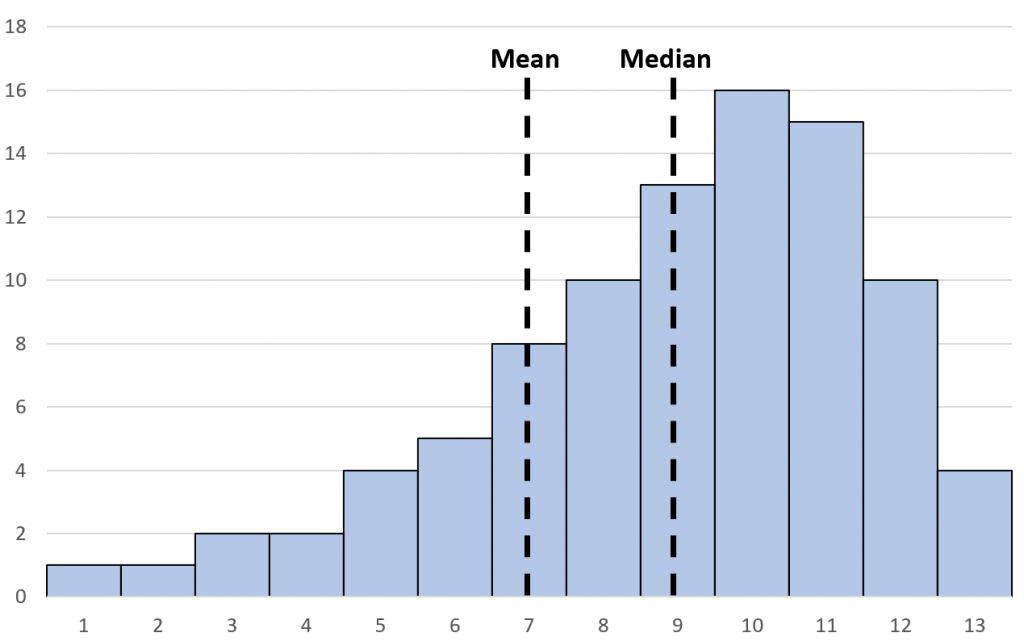
In the realm of statistics, the phrase takes on additional meaning. When analyzing data distributions, one may encounter scenarios where the mean is less than the median, indicating a left-skewed distribution. Such scenarios are instrumental in interpreting data trends, providing insights into anomalies and general tendencies within datasets. Here, “less than” transcends mere numerical comparison, entering the discourse of data interpretation and statistical significance.
Furthermore, the term “less than” can evoke qualitative comparisons as well. In discussions regarding preferences or assessments, individuals may express that one choice is less than another in terms of desirability or quality. For instance, one might argue that option A is less than option B, thereby imparting a subjective valuation that reflects personal or collective standards. This application is especially prominent in fields like marketing, where consumer preferences are quantified to gauge product appeal.
Moreover, “less than” can facilitate the understanding of thresholds, where certain limits define acceptable boundaries within disciplines. In ethics, a principle might state that one action is less than acceptable in comparison to another, influencing moral judgment and societal standards. In economics, cost analysis could reflect how the expenditure for one product is less than that of another, influencing consumer choices and market dynamics.
Overall, the phrase “less than” encapsulates both quantitative and qualitative dimensions, guiding interpretations across varied fields. Its implications stretch from basic arithmetic to complex analytic frameworks, revealing the versatile and essential nature of comparative analysis in understanding the world around us.